14  Accessibility

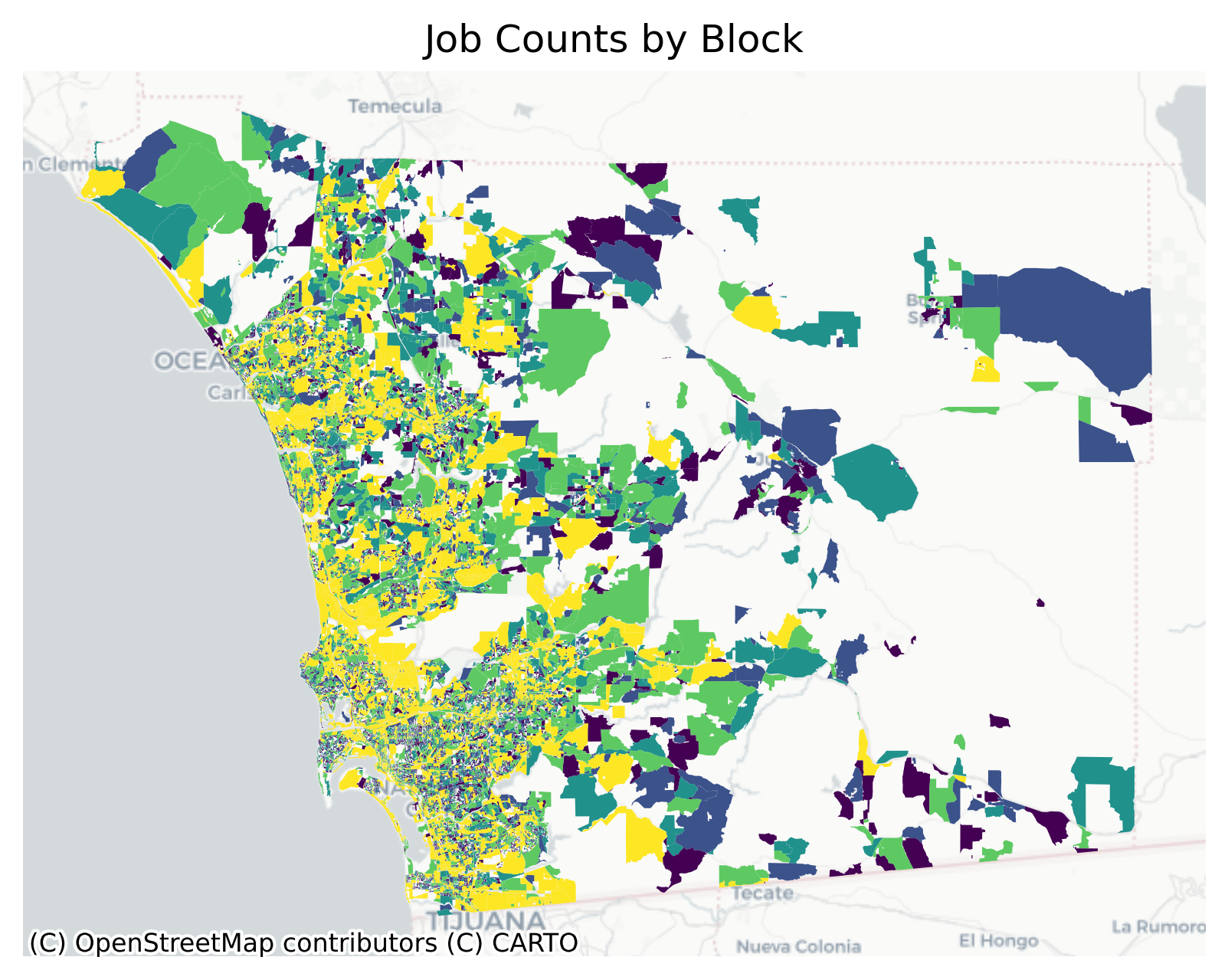
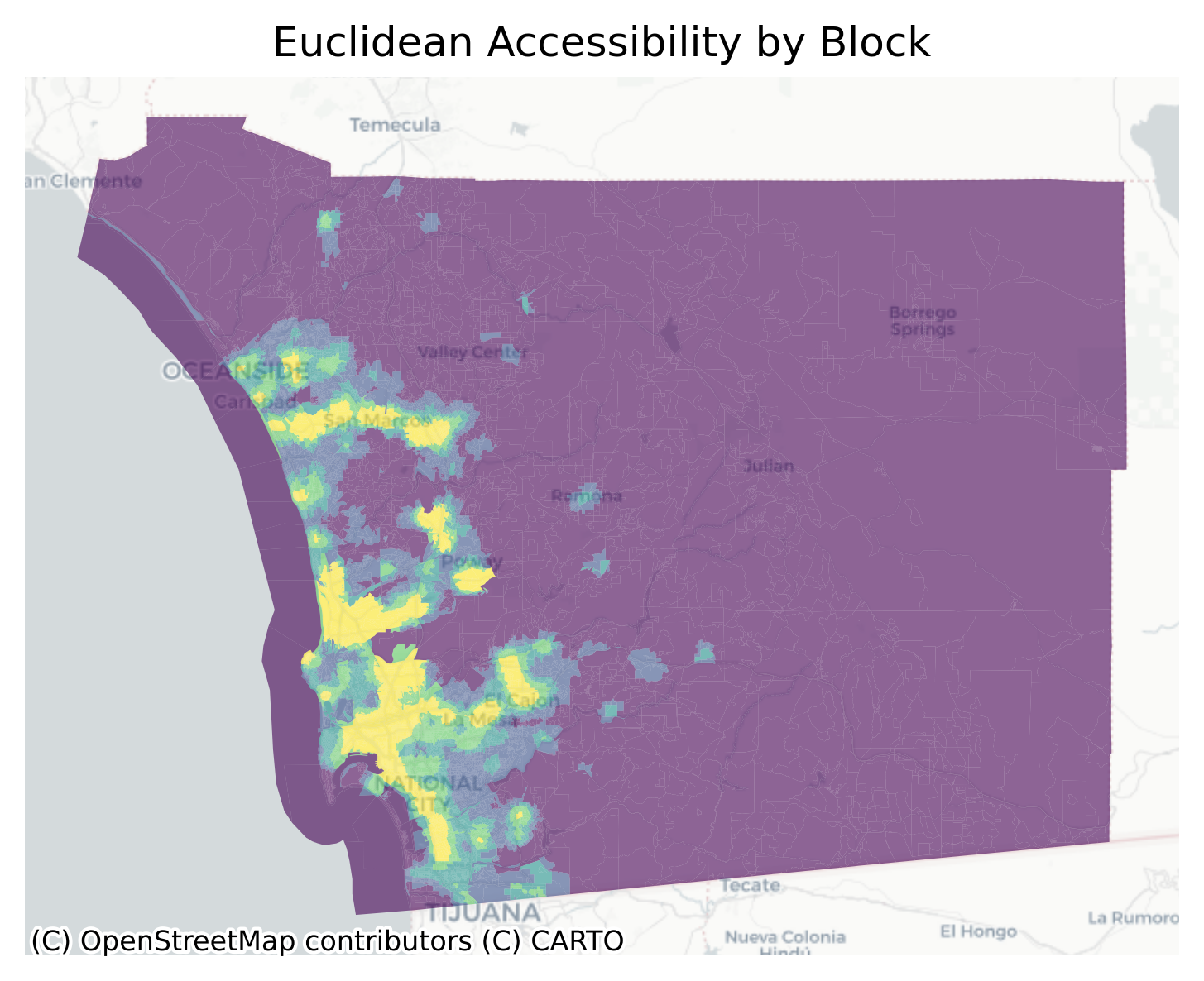
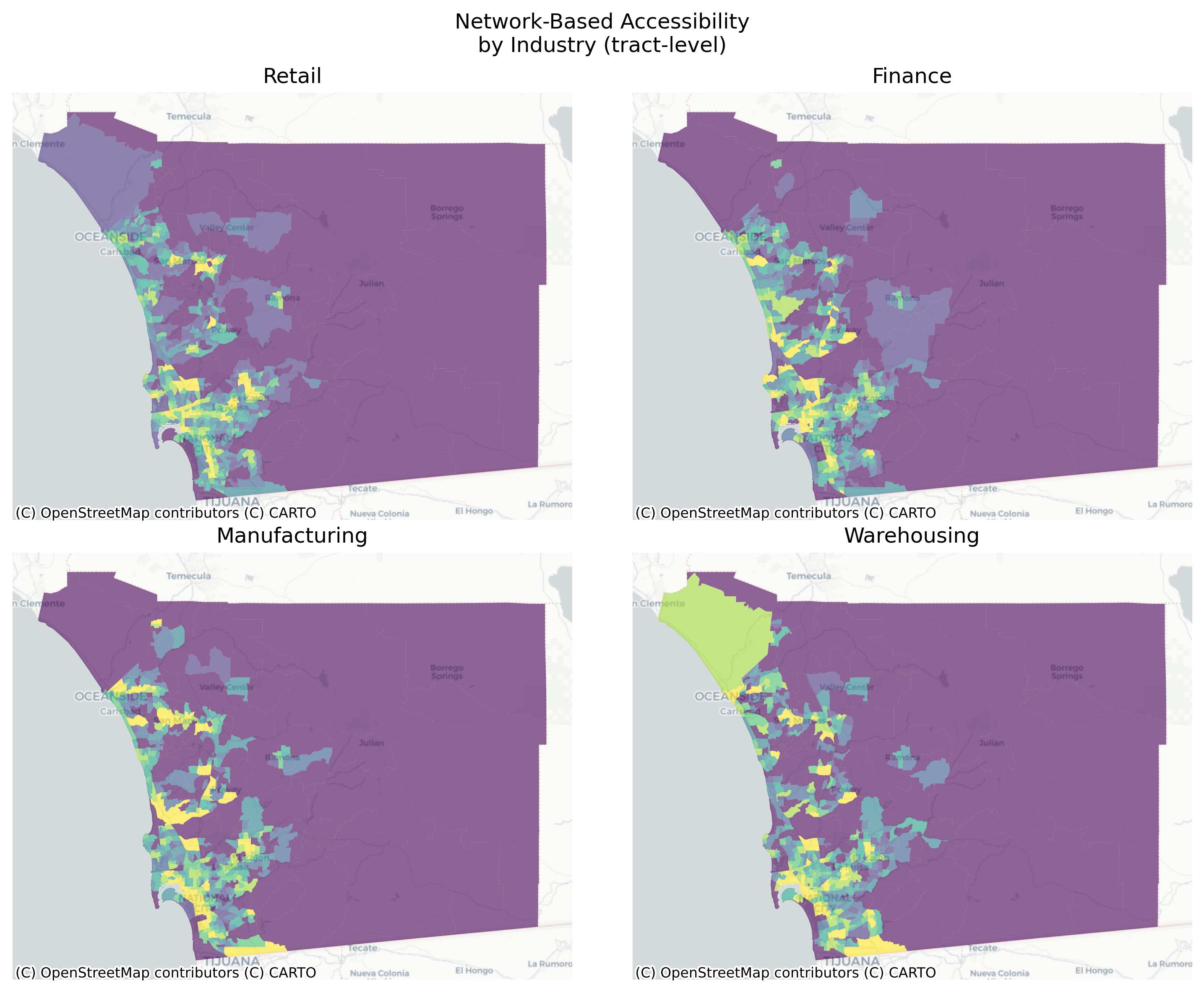
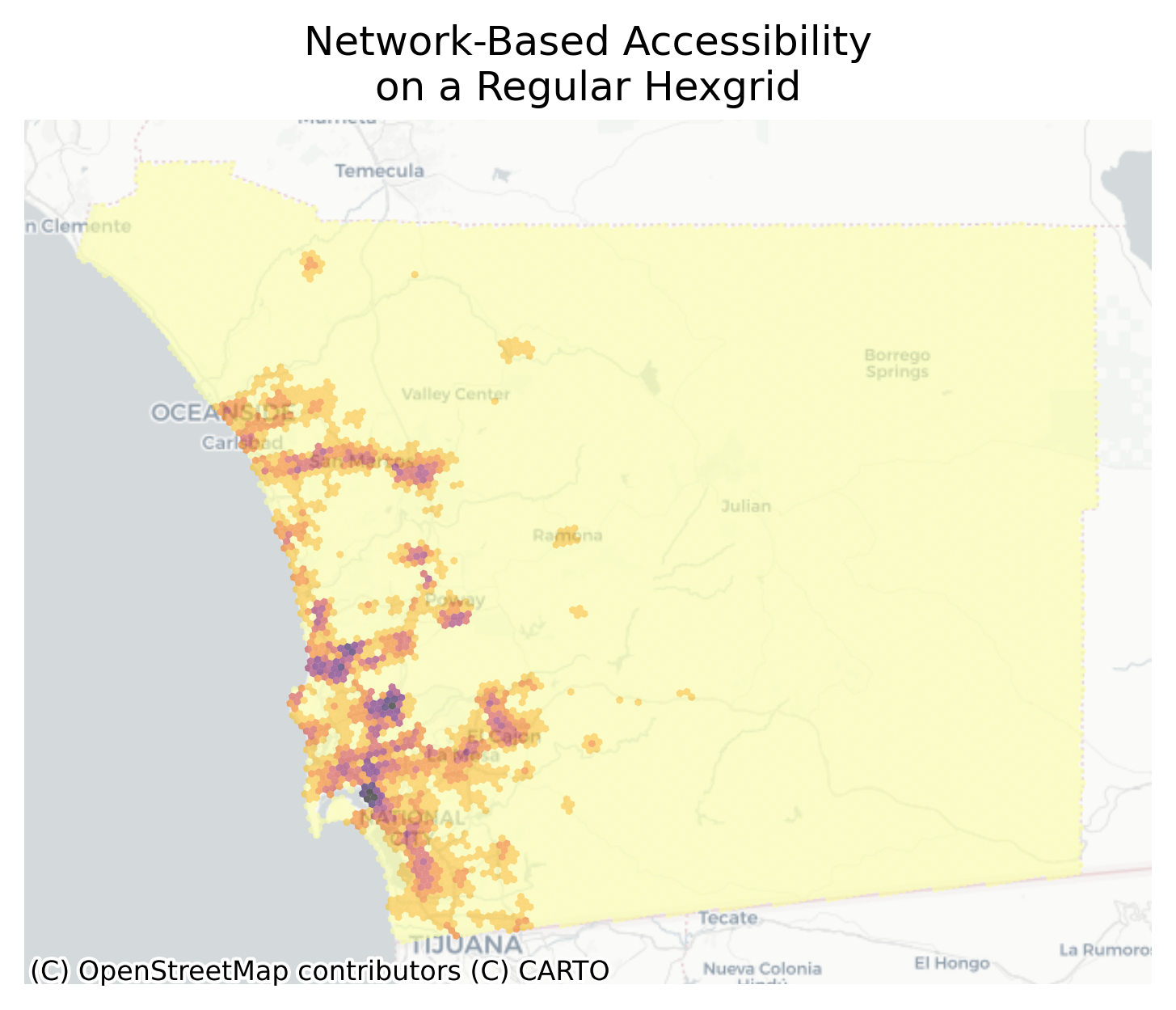
Code 
import contextily as ctx
import geopandas as gpd
import mapclassify as mc
import matplotlib.pyplot as plt
import numpy as np
import pandana as pdna
import pandas as pd
import pydeck as pdk
import quilt3 as q3
from geosnap import DataStore
from geosnap import analyze as gaz
from geosnap import io as gio
from libpysal.graph import Graph
from matplotlib import cm
from matplotlib.colors import Normalize
from tobler.util import h3fy

%load_ext watermark
%watermark -a 'eli knaap'  -iv
OMP: Info #276: omp_set_nested routine deprecated, please use omp_set_max_active_levels instead.
Author: eli knaap

geopandas  : 0.14.4
geosnap    : 0.12.1.dev9+g3a1cb0f6de61.d20240110
quilt3     : 5.0.0
pandana    : 0.7
pandas     : 1.5.3
mapclassify: 2.6.1
contextily : 1.5.2
pydeck     : 0.8.0b4
matplotlib : 3.4.3
numpy      : 1.23.5

14.1 Access, Gravity, & Spatial Interaction

Accessibility is a recurrent theme in urban social science (El-Geneidy & Levinson, 2006; Fotheringham, 1981; Hansen, 1959; Huff, 1963; Levinson et al., 2017; Levinson & Wu, 2020; Kumar1994?). The original concept deals with access to employment and is used to help explain the size and layout of a city (Converse, 1949; Huff, 1962, 1964, 1966); this thread grew into an entire field of spatial interaction and continues to be the heart of travel demand modeling. More recently, accessibility analysis has become an important part of social equity analysis (e.g., to show whether certain population groups have better or worse access to a particular resource, a la the spatial mismatch hypothesis). This thread has been particularly strong in health geography where several new accessibility concepts have been proposed (Luo & Wang, 2003; Wang, 2012, 2021; Wang & Luo, 2005).

If we combine the intuition with Zipf (1949) with Stewart & Warntz (1958) and Stewart (1947), it amounts to a behavioral explanation for why humans behave like particles in some cases.

The “demographic gravitation” implied by various applications of the concept of potential of population serves to account in part for these facts. But a statistical countertendency is required to explain why all the people in a city do not pile up in the most dense census tract. An adequate mathematical description of this appears to be found in the concept of the “human gas.” Each individual seeks some elbowroom or living space. The idea of a two-dimensional gas is already familiar in physics (monomolecular layers). In the demographic analogue we write: pa = NT, where a is the area occupied by N individuals (molecules), p is the “demographic pressure,” and T is the “demographic temperature.” In the physical case, p is the force per unit length of boundary.

– Stewart (1947)

In other words, people enjoy personal space–and they are lazy, but are nonetheless drawn to collections of resources; the larger the concentration, the stronger the pull, but increasing distance attenuates that attraction. Thus, ‘accessibility’ effectively operationalizes the concept of distance decayed attraction, which is just like the gravity equation in physics.

Finally, the gravity concept is essentially an empirical notion. It tells nothing about why observed regularities occur as they do under various situations and, as a consequence, it leaves one at a loss when discrepancies occur that cannot be accounted for. Yet, it is surprising to note how often gravity models pertaining to human interaction are referred to as laws or theories. These models are nothing more than tools that allow one to make short-cut approximations of the direction and magnitude of individual travel movement

– Huff (1962)

Anas (1983) later formulated a behavioral explanation for the gravity model, specifically that the doubly-constrained gravity model is equivalent to a multinomial logit model of joint origin-destination choice. This cements an actual behavioral explanation for the gravity model rooted in utility maximization. As such access to destinations will be explored as a primary driver of location choice in later sections.

The basic form of an access measure following Hansen (1959) is

\[ A_i = \sum_{j=1}^J O_j f(C_{ij}) \]

Where the accessibility measure \(A\) at location \(i\) is a sum of the opportunities \(O\) available at \(j\) locations, weighted by some function of the cost of moving from \(i\) to \(j\). Generally \(f(C_{ij})\) is an exponential decay function where cost \(C\) is measured in some form of travel impedance like network distance or travel time (Levinson & Wu, 2020). That is, \(C_{ij}\) is a special case of the spatial graph where we also care about the values located at \(i\) itself (\(C_{ii} \neq 0\))(Knaap & Rey, 2023). As we saw in Chapter 1, it is trivial to create a simple accessibility measure using a Graph.

Thus, if this looks like the spatial lag equation from Chapter 10, that’s because it is. The differences are

  1. here we consider a unit part of its own context (i.e. we allow \(i=j\)) and
  2. unlike the spatial lag, we do not row-standardize the cost matrix (so \(A_i\) remains a distance-weighted sum, not an average)

14.2 Job Access in San Diego

We start by gathering employment data from LODES for the San Diego metropolitan region via geosnap. The LODES data tabulate block-level counts of employees at their workplace and residential locations (also broken out by wage, education, race, sex, and industry). Since we are interested in access to jobs, we will assume each employee represents one job (which is located at the workplace area according to LODES). For convenient visualization (because blocks can often crash the browser) we will also load in the census tract boundaries.

Code 
datasets = DataStore()

sd_acs = gio.get_acs(datasets, county_fips="06073", years=[2021], level="tract")
sd_lodes = gio.get_lodes(datasets, county_fips="06073", years="2021")
/Users/knaaptime/Dropbox/projects/geosnap/geosnap/io/util.py:275: UserWarning: Unable to find local adjustment year for 2021. Attempting from online data
  warn(
/Users/knaaptime/Dropbox/projects/geosnap/geosnap/io/constructors.py:215: UserWarning: Currency columns unavailable at this resolution; not adjusting for inflation
  warn(
Code 
ax = sd_lodes.to_crs(3857).plot("total_employees", scheme="quantiles")
ctx.add_basemap(ax, source=ctx.providers.CartoDB.Positron)
ax.axis("off")
ax.set_title("Job Counts by Block")
Text(0.5, 1.0, 'Job Counts by Block')

Because of the irregular size and shape of census blocks, it is difficult to discern any real pattern from a simple choropleth map of employment counts, but there is a strong signal laying under the surface.

14.2.1 Euclidean Distance

Code 
g = Graph.build_kernel(
    sd_lodes.to_crs(sd_lodes.estimate_utm_crs()).centroid,
    bandwidth=2000,
    kernel="triangular",
)
Code 
g = g.assign_self_weight(1)
Code 
A = g.lag(sd_lodes.total_employees.fillna(0))
Code 
A
array([ 9112.54368043,  9300.15381342, 10143.84732735, ...,
           0.        ,     0.        ,  2094.21502562])
Code 
ax = (
    sd_lodes.assign(access=A)
    .to_crs(3857)
    .plot("access", scheme="quantiles", alpha=0.6, figsize=(8, 7))
)
ctx.add_basemap(ax, source=ctx.providers.CartoDB.Positron)
ax.set_title("Euclidean Accessibility by Block")
ax.axis("off")
(-13100922.374414548,
 -12913554.405756447,
 3826449.938821171,
 3969011.1015594862)

14.2.2 Network Distance

As we saw in Chapter 9, it is important to consider travel network impedance as a distance measure in urban spaces where Euclidean proxies often fail (Knaap & Rey, 2023). To account for that we use the pandana package (Foti et al., 2012) which implements the contraction hierarchies technique (Geisberger et al., 2012) for quickly computing shortest path distances along the network. To compute access measures based on the shortest path distance, we first need a network that represents the study area. You can create your own network on the fly from OpenStreetMap using either geosnap’s network module or osmnet. Alternatively you can use a pre-constructed network (based on OSM), e.g. those stored in the geosnap quilt bucket.

Using a pre-constructed network, we instantiate by reading from an hdf5 file.

Code 
b = q3.Bucket("s3://spatial-ucr")
b.fetch("osm/metro_networks_8k/41740.h5", "../data/41740.h5")
100%|██████████| 29.2M/29.2M [00:02<00:00, 13.8MB/s]
Code 
sd_network = pdna.Network.from_hdf5("../data/41740.h5")
Generating contraction hierarchies with 10 threads.
Setting CH node vector of size 332554
Setting CH edge vector of size 522484
Range graph removed 143094 edges of 1044968
. 10% . 20% . 30% . 40% . 50% . 60% . 70% . 80% . 90% . 100%

Following, we need to connect the network to the data we want to measure and visualize, which is accomplished by snapping the source data to their nearest intersections in the Network. The Network.get_node_ids function takes care of that and returns an index (representing the node ID of the network intersection) for each input observation (here, the centroid of each census block) thus mapping the job data to the travel network. It is a good idea to save these IDs as a variable on the input dataframe so we can use them as a join index

Code 
nodes = sd_network.get_node_ids(
    sd_lodes.centroid.geometry.x, sd_lodes.centroid.geometry.y
)

# get the node ids for tracts also (for visualization)
tract_nodes = sd_network.get_node_ids(
    sd_acs.centroid.geometry.x, sd_acs.centroid.geometry.y
)

sd_lodes["node_ids"] = nodes
sd_acs["node_ids"] = tract_nodes
/var/folders/79/cknfb1sx2pv16rztkpg6wzlw0000gn/T/ipykernel_13659/1286788151.py:2: UserWarning: Geometry is in a geographic CRS. Results from 'centroid' are likely incorrect. Use 'GeoSeries.to_crs()' to re-project geometries to a projected CRS before this operation.

  sd_lodes.centroid.geometry.x, sd_lodes.centroid.geometry.y
/var/folders/79/cknfb1sx2pv16rztkpg6wzlw0000gn/T/ipykernel_13659/1286788151.py:7: UserWarning: Geometry is in a geographic CRS. Results from 'centroid' are likely incorrect. Use 'GeoSeries.to_crs()' to re-project geometries to a projected CRS before this operation.

  sd_acs.centroid.geometry.x, sd_acs.centroid.geometry.y
Code 
nodes
0          49687557
1          49594127
2        3701750397
3          49594127
4          49132756
            ...    
28628      49384075
28629    6504175127
28630    5554890554
28631    2373270861
28632    5833546523
Name: node_id, Length: 28633, dtype: int64

With locations set, we now need to attach values to the network (i.e. the amount of “resources” located at each node in the network). The LODES data contain information on many subsets of jobs

Code 
sd_lodes.columns
Index(['geoid', 'year', 'CFA01', 'CFA02', 'CFA03', 'CFA04', 'CFA05', 'CFS01',
       'CFS02', 'CFS03', 'CFS04', 'CFS05', 'aland20', 'awater20',
       'create_date', 'earnings_1251_3333', 'earnings_over_3333',
       'earnings_under_1250', 'education_bachelors', 'education_hs',
       'education_lths', 'education_some_college', 'employees_30_54',
       'employees_55plus', 'employees_asian', 'employees_black',
       'employees_female', 'employees_hawaiian_pi', 'employees_hispanic',
       'employees_male', 'employees_native_american', 'employees_not_hispanic',
       'employees_twoplus_races', 'employees_under_30', 'employees_white',
       'geometry', 'housing_units', 'naics_11', 'naics_21', 'naics_22',
       'naics_23', 'naics_31_33', 'naics_42', 'naics_44_45', 'naics_48_49',
       'naics_51', 'naics_52', 'naics_53', 'naics_54', 'naics_55', 'naics_56',
       'naics_61', 'naics_62', 'naics_71', 'naics_72', 'naics_81', 'naics_92',
       'population', 'total_employees', 'node_ids'],
      dtype='object')

Since we only need the columns with NAICS codes, we can filter down the codebook to show only those rows we care about (to see what the codes actually mean). The North American Industry Classification System (NAICS) is a taxonomy for identifying jobs in particular industries. As with a FIPS code, NAICS is hierarchical, with each additional digit in the code providing an additional level of detail in the industrial makeup. The two-digit classifications provide a generic overview of different industries allowing us to examine, for example whether access to manufacturing jobs differs from access to retail employment.

Code 
# add some width in in the display so we can see the full description
pd.options.display.max_colwidth = 100

lodes_codebook = datasets.lodes_codebook()
lodes_codebook[lodes_codebook["name"].str.contains("naics")]
name variable type description
7 naics_11 CNS01 Num Number of jobs in NAICS sector 11 (Agriculture, Forestry, Fishing and Hunting)
8 naics_21 CNS02 Num Number of jobs in NAICS sector 21 (Mining, Quarrying, and Oil and Gas Extraction)
9 naics_22 CNS03 Num Number of jobs in NAICS sector 22 (Utilities)
10 naics_23 CNS04 Num Number of jobs in NAICS sector 23 (Construction)
11 naics_31_33 CNS05 Num Number of jobs in NAICS sector 31-33 (Manufacturing)
12 naics_42 CNS06 Num Number of jobs in NAICS sector 42 (Wholesale Trade)
13 naics_44_45 CNS07 Num Number of jobs in NAICS sector 44-45 (Retail Trade)
14 naics_48_49 CNS08 Num Number of jobs in NAICS sector 48-49 (Transportation and Warehousing)
15 naics_51 CNS09 Num Number of jobs in NAICS sector 51 (Information)
16 naics_52 CNS10 Num Number of jobs in NAICS sector 52 (Finance and Insurance)
17 naics_53 CNS11 Num Number of jobs in NAICS sector 53 (Real Estate and Rental and Leasing)
18 naics_54 CNS12 Num Number of jobs in NAICS sector 54 (Professional, Scientific, and Technical Services)
19 naics_55 CNS13 Num Number of jobs in NAICS sector 55 (Management of Companies and Enterprises)
20 naics_56 CNS14 Num Number of jobs in NAICS sector 56 (Administrative and Support and Waste Management and Remediati...
21 naics_61 CNS15 Num Number of jobs in NAICS sector 61 (Educational Services)
22 naics_62 CNS16 Num Number of jobs in NAICS sector 62 (Health Care and Social Assistance)
23 naics_71 CNS17 Num Number of jobs in NAICS sector 71 (Arts, Entertainment, and Recreation)
24 naics_72 CNS18 Num Number of jobs in NAICS sector 72 (Accommodation and Food Services)
25 naics_81 CNS19 Num Number of jobs in NAICS sector 81 (Other Services [except Public Administration])
26 naics_92 CNS20 Num Number of jobs in NAICS sector 92 (Public Administration)

Following we can select a few different industries and examine access to each of them and whether the patterns differ

Code 
sd_network.set(nodes, sd_lodes.total_employees.values, name="jobs")
sd_network.set(nodes, sd_lodes.naics_44_45.values, name="retail")
sd_network.set(nodes, sd_lodes.naics_52.values, name="finance")
sd_network.set(nodes, sd_lodes.naics_31_33.values, name="manufacturing")
sd_network.set(nodes, sd_lodes.naics_48_49.values, name="warehousing")
Removed 12657 rows because they contain missing values
Removed 12657 rows because they contain missing values
Removed 12657 rows because they contain missing values
Removed 12657 rows because they contain missing values
Removed 12657 rows because they contain missing values

Accessibility measures are generated with pandana using an “aggregation query” where we define:

  • the variable of interest
  • the form of the decay function (flat, linear, exponential)
  • the bandwidth/radius of the decay function
  • the aggregation to perform (sum, average, quantile, etc. A standard access measure is based on a distance-weighted sum)

So here, we look at access to total jobs using a distance-weighted sum with a decay up to 2000 meters. We can create two separate measures based on different decay functions (exponential and linear)

Code 
job_access = sd_network.aggregate(2000, name="jobs")  # linear decay
job_access_exp = sd_network.aggregate(
    2000, name="jobs", decay="exp"
)  # exponential decay
Code 
job_access
id
17413808       411.665598
17413859         0.000000
28828453       294.682681
48857408       696.974011
48857412       500.270295
                 ...     
6568745422       0.000000
6568761537       0.000000
6568761541       0.000000
6568829948    7023.202896
6568913078       0.000000
Length: 332554, dtype: float64

Then, we repeat that process for each of the industries we would like to compare. In this case we will use an exponential decay for all measures.

Code 
dfs = {}
dests = ["retail", "finance", "manufacturing", "warehousing"]
for dest in dests:
    dfs[dest] = sd_network.aggregate(2000, name=dest, decay="exp")

The resulting dataframe stores accessibility measures for each intersection in the pandana.Network, which means access is captured at an extremely high resolution (of course this is also dependent on the spatial resolution of the input data, which were Census blocks in this case, and also have very high resolution)

Code 
ac = pd.DataFrame(dfs)
ac
retail finance manufacturing warehousing
id
17413808 0.000000 0.000000 0.000000 53.000000
17413859 0.000000 0.000000 0.000000 0.000000
28828453 88.027798 1.290641 3.441710 4.732352
48857408 70.768797 51.878775 205.081798 99.457479
48857412 105.573721 26.980106 2.812058 1.504362
... ... ... ... ...
6568745422 0.000000 0.000000 0.000000 0.000000
6568761537 0.000000 0.000000 0.000000 0.000000
6568761541 0.000000 0.000000 0.000000 0.000000
6568829948 1537.976564 70.259058 400.737876 442.950873
6568913078 0.000000 0.000000 0.000000 0.000000

332554 rows × 4 columns

Following, we can merge these variables back onto a geodataframe and visualize the results.

Code 
sd_acs = sd_acs.merge(
    job_access.rename("job_access"), left_on="node_ids", right_index=True
)

sd_acs = sd_acs.merge(
    job_access_exp.rename("job_access_exp"), left_on="node_ids", right_index=True
)

sd_acs = sd_acs.merge(ac, left_on="node_ids", right_index=True)
Code 
f, ax = plt.subplots(2, 2, figsize=(10, 8))
ax = ax.flatten()
for i, dest in enumerate(dests):

    sd_acs[sd_acs.n_total_pop > 0].to_crs(3857).plot(
        dest, scheme="quantiles", k=8, alpha=0.6, ax=ax[i]
    )
    ax[i].axis("off")
    ax[i].set_title(dest.title())
    ctx.add_basemap(ax[i], source=ctx.providers.CartoDB.Positron)
plt.suptitle("Network-Based Accessibility\nby Industry (tract-level)")
plt.tight_layout()

Code 
sd_acs[sd_acs.n_total_pop > 0].explore(
    "job_access_exp",
    scheme="quantiles",
    k=6,
    tooltip="job_access",
    tiles="CartoDB Positron",
)
Make this Notebook Trusted to load map: File -> Trust Notebook

14.3 Better Visualization

The accessibility measures are captured at the intersection level, but thus far we have been using census geometries to visualize the values. As such, there are several ways we can improve the accessibility visualization, some conceptual, some practical (given our technology). First, we can move to a higher resolution, since the data are captured at that level. Second, we can use a different (more uniform in this case) set of polygons. In this example, the eye tends to be drawn to the large rural polygons simply because they are larger than the small, denser tracts in the urban core. That is also useful because simpler polygons have fewer vertices and are easier to render in the browser. Finally, this is a case where including another dimension (the z-dimension or height) can be useful because it allows a more continuous visualization of the accessibility distribution.

PyDeck can generate some visualizations on the fly, but only if you have multiple observations at the same location. Here, we need to create the visualization ourselves, so we first generate a hexgrid that covers the study area, then attach the access values to those polygons and extrude them using PyDeck

Code 
hexes = h3fy(sd_acs[sd_acs.n_total_pop > 0], resolution=8)
Code 
hexes.plot()

Code 
hexes["node_ids"] = sd_network.get_node_ids(
    hexes.centroid.geometry.x, hexes.centroid.geometry.y
)
/var/folders/79/cknfb1sx2pv16rztkpg6wzlw0000gn/T/ipykernel_13659/2358585746.py:2: UserWarning: Geometry is in a geographic CRS. Results from 'centroid' are likely incorrect. Use 'GeoSeries.to_crs()' to re-project geometries to a projected CRS before this operation.

  hexes.centroid.geometry.x, hexes.centroid.geometry.y
Code 
hexes = hexes.merge(
    job_access_exp.rename("job_access"), left_on="node_ids", right_index=True
)
Code 
ax = (
    hexes.fillna(0)
    .to_crs(3857)
    .plot(
        "job_access",
        scheme="fisher_jenks",
        k=8,
        cmap="inferno_r",
        alpha=0.6,
        figsize=(8, 7),
    )
)

ctx.add_basemap(ax, source=ctx.providers.CartoDB.Positron)
ax.set_title("Network-Based Accessibility\non a Regular Hexgrid")
ax.axis("off")

Code 
hexes.fillna(0).to_crs(3857).explore(
    "job_access",
    scheme="fisher_jenks",
    k=8,
    cmap="inferno_r",
    tiles="CartoDB Positron",
    tooltip="job_access",
    style_kwds={"fill_opacity": 0.8, "weight": 0},
)
Make this Notebook Trusted to load map: File -> Trust Notebook

14.3.1 Using the Z-Dimension

Code 
var = "job_access"
classifier = "fisherjenks"
k = 8
cmap = "inferno_r"
Code 
def get_height(val):
    return val**0.9
Code 
def get_color(
    array, classifier="quantiles", k=6, cmap="viridis", fillcolor=[255, 255, 255, 255]
):

    v = pd.Series(array)
    legit_indices = v[~v.isna()].index.values

    # transform (non-NaN) values into class bins
    bins = mc.classify(v.dropna().values, scheme=classifier, k=k).yb

    # create a normalizer using the data's range (not strictly 1-k...)
    norm = Normalize(min(bins), max(bins))

    # map values to colors
    n_cmap = cm.ScalarMappable(norm=norm, cmap=cmap)

    # create array of RGB values (lists of 4) of length n
    vals = [n_cmap.to_rgba(i, alpha=None) for i in bins]

    # convert decimals to whole numbers
    rgbas = []
    for val in vals:
        # convert each value in the array of lists
        rgbas.append([round(i * 255, 0) for i in val])

    # replace non-nan values with colors
    colors = pd.Series(rgbas, index=legit_indices)
    v.update(colors)
    v = v.fillna(f"{fillcolor}").apply(list)

    return v.values

With those functions in hand, we can create two temporary ‘visualization variables’ that can be passed to the PyDeck plot function. Note when creating the fill_color variable below I am temporarily filling NaN values with zero. This ensures all values are assigned into classes, otherwise the mapclassify classifier will fail–but this is also just a convenient fix because it technically invalidates the classification scheme. By treating NaN values as true zeros (as opposed to dropping them as unknown information), we change the distribution by allowing those zeros to help define the quantile bins.

Code 
hexes["fill_color"] = get_color(hexes[var], classifier, k, cmap)
hexes["height"] = hexes[var].apply(lambda x: get_height(x))
Code 
layers = [
    pdk.Layer(
        "GeoJsonLayer",
        data=hexes[["geometry", "fill_color", "job_access", "height"]],
        get_fill_color="fill_color",
        opacity=0.6,
        extruded=True,
        get_elevation="height",
        auto_highlight=True,
        pickable=True,
    ),
]

view_state = pdk.ViewState(
    **{  # pull the camera to the southwest
        "latitude": hexes.unary_union.centroid.y - 0.15,
        "longitude": hexes.unary_union.centroid.x - 0.25,
        "zoom": 8.8,
        "maxZoom": 16,
        "pitch": 50,
        "bearing": 50,
    }
)

D = pdk.Deck(
    layers,
    map_provider="carto",
    map_style=pdk.map_styles.LIGHT,
    height=700,
    initial_view_state=view_state,
)
Code 
D

Again, dragging in the map using option+click allows you to change the camera orientation rather than pan

In San Diego, the largest concentrations of accessibility are Downtown, Kerney Mesa, and Torrey Pines/University City/Sorrento Valley triangle–three of the largest employment centers in the region (explored more in Chapter 17). And using the 3D extrusion, it is easy to see how these places compare in magnitude to other ‘high access’ places in the region further inland, like Escondido, Poway, and El Cajon.

:::