[[24]{.chapter-number}  [Regionalization ]{.chapter-title}]{#sec-regionalization .quarto-section-identifier}

24 Regionalization

Code

import contextily as ctx
import geopandas as gpd
import matplotlib.pyplot as plt
from geosnap import DataStore
from geosnap import analyze as gaz
from geosnap import io as gio
from geosnap import visualize as gvz

%load_ext watermark
%watermark -a  'eli knaap' -iv -d -u

OMP: Info #276: omp_set_nested routine deprecated, please use omp_set_max_active_levels instead.

Author: eli knaap

Last updated: 2025-11-25

matplotlib: 3.10.8
geosnap   : 0.15.3
geopandas : 1.1.1
contextily: 1.6.2

As with geodemographic clustering, when carrying out a regionalization exercise, we are searching for groups of observations (census tracts in this case) which are similar in socioeconomic and demographic composition. If the goal of geodemographics is to identify neighborhood types, that could exist anywhere in the region, the goal of regionalization is to identify specific neighborhoods that exist at a distinct place in the region

Following that concept, we can use constrained clustering to develop an empirical version of geographically-bounded neighborhoods, where the neighborhoods are defined by internal social homogeneity. This is similar to the historic and well-defined neighborhood zones in places like Chicago and Pittsburgh. If your goal were to try and delineate neighborhoods in a bespoke region as the LA Times tried to do, regionalization would be a data-driven way to do so.

https://en.wikivoyage.org/wiki/File:Chicago_neighborhoods_map.png

https://www.visitpittsburgh.com/neighborhoods

Code

datasets = DataStore()
la = gio.get_acs(datasets, county_fips="06037", years=2021, level="tract")
la = la.to_crs(la.estimate_utm_crs())

la[["median_household_income", "geometry"]].explore(
    "median_household_income",
    scheme="quantiles",
    k=8,
    cmap="magma",
    tiles="CartoDB Positron",
)

columns = [
    "median_household_income",
    "median_home_value",
    "p_edu_college_greater",
    "p_edu_hs_less",
    "p_nonhisp_white_persons",
    "p_nonhisp_black_persons",
    "p_hispanic_persons",
    "p_asian_persons",
]
la.dropna(subset=columns).plot()

/Users/knaaptime/miniforge3/envs/urban_analysis/lib/python3.12/site-packages/geosnap/io/util.py:273: UserWarning: Unable to find local adjustment year for 2021. Attempting from online data
  warn(
/Users/knaaptime/miniforge3/envs/urban_analysis/lib/python3.12/site-packages/geosnap/io/constructors.py:218: UserWarning: Currency columns unavailable at this resolution; not adjusting for inflation
  warn(

24.1 Cross-Sectional Regionalization

Similar to Chapter 23, we begin by loading Census data (this time from the Los Angeles metropolitan region), then generate a typology or set of regions by passing a collection of variables to the regionalize function from geosnap. In this instance, we will create 25 regions using spatially-constrained hierarchical clustering (using Ward’s linkage). Since the regionalization technique enforces a spatial constraint, we also need to pass a libpysal Graph or spatial weights object; alternatively, we can pass the name of a contiguity Graph, like “rook” or “queen”.

Code

la_ward_reg, la_ward_model = gaz.regionalize(
    gdf=la,
    method="ward_spatial",
    n_clusters=25,
    columns=columns,
    return_model=True,
    spatial_weights="queen",
)
la_ward_reg[columns + ["geometry", "ward_spatial"]].explore(
    "ward_spatial", categorical=True, cmap="Accent", tiles="CartoDB Positron"
)

/Users/knaaptime/miniforge3/envs/urban_analysis/lib/python3.12/site-packages/geosnap/analyze/geodemo.py:406: FutureWarning: `use_index` defaults to False but will default to True in future. Set True/False directly to control this behavior and silence this warning
  w0 = W.from_dataframe(df, **weights_kwargs)
/Users/knaaptime/miniforge3/envs/urban_analysis/lib/python3.12/site-packages/libpysal/weights/contiguity.py:347: UserWarning: The weights matrix is not fully connected: 
 There are 4 disconnected components.
 There are 2 islands with ids: 568, 1944.
  W.__init__(self, neighbors, ids=ids, **kw)

Make this Notebook Trusted to load map: File -> Trust Notebook

Code

ax = la_ward_reg[columns + ["geometry", "ward_spatial"]].plot(
    "ward_spatial", categorical=True, cmap="Accent", figsize=(6, 6), alpha=0.6
)
ax.axis("off")
ctx.add_basemap(ax=ax, source=ctx.providers.CartoDB.Positron, crs=la_ward_reg.crs)
plt.show()

Unlike the general clustering case, regionalization algorithms can only group together observations that are connected via a spatial connectivity graph. That means the map is much more distinctive, but the resulting clusters are usually far less homogenous internally than the unconstrained case. Also, in some cases, the use of a Queen Graph can result in long and spindly “regions,” rather than dense, compact ones because observations can string along corridors by connecting through the corners of each input polygon.

To understand what the clusters are identifying, another data visualisation technique is useful. Here, we rely on the Tufte-ian principle of “small multiples”, and create a set of violin plots that show how each variable is distributed across each of the clusters. Each of the inset boxes shows a different variable, with cluster assignments on the x-axis, and the variable itself on the y-axis The boxplot in the center shows the median and IQR, and the “body” of the “violin” is a kernel-density estimate reflected across the x-axis. In short, the fat parts of the violin show where the bulk of the observations are located, and the skinny “necks” show the long tails.

Code

gvz.plot_violins_by_cluster(la_ward_reg, columns, cluster_col="ward_spatial")
plt.show()

Notice here that the violin plots are much harder to distinguish. That is, by enforcing a contiguity constraint, many census tracts are grouped with other tracts that they are closest to, rather than those they are most similar to in multivariate attribute space. This is reflected in the silhouette scores as well. Unlike the general clustering case, regionalization algorithms return a dictionary of ModelResults classes (one for each unique time period in the dataset) because it is not possible to create a pooled regionalization solution using data from multiple time periods

Code

la_ward_model

{np.int64(2021): <geosnap.analyze._model_results.ModelResults at 0x34a480f80>}

Code

la_ward_model[2021].plot_silhouette()
plt.show()

This is a poor silhouette score indeed–the overall score for the solution is negative, meaning most tracts are more similar (in attributes) to tracts in another cluster than the one they are assigned. But a silhouette score is not the ideal metric in this case, because attribute similarity is no longer the only objective the model is trying to achieve.

Code

la_ward_model[2021].plot_silhouette_map(figsize=(7, 7))
plt.show()

/Users/knaaptime/miniforge3/envs/urban_analysis/lib/python3.12/site-packages/geosnap/visualize/mapping.py:171: UserWarning: `proplot` is not installed.  Falling back to matplotlib
  warn("`proplot` is not installed.  Falling back to matplotlib")

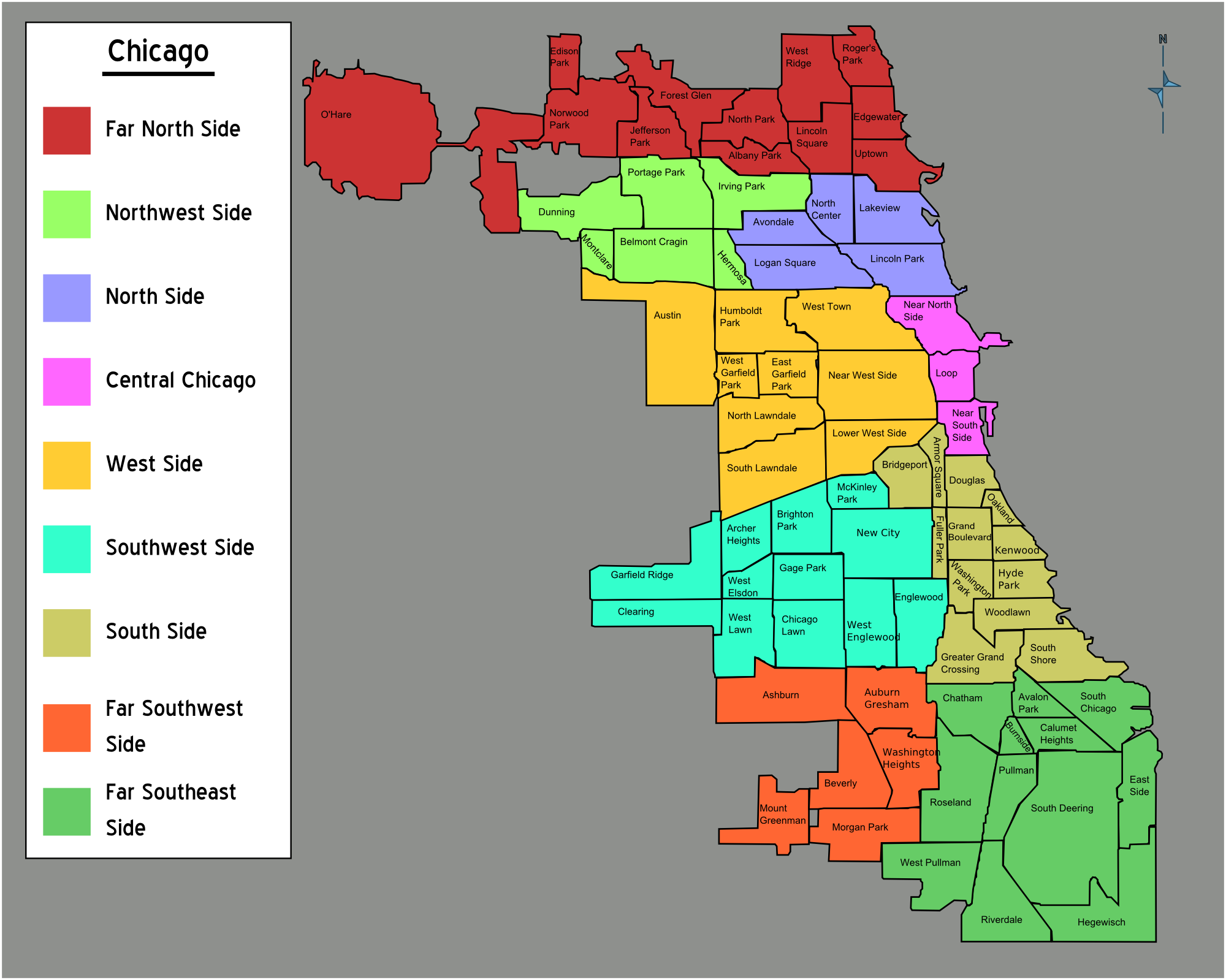
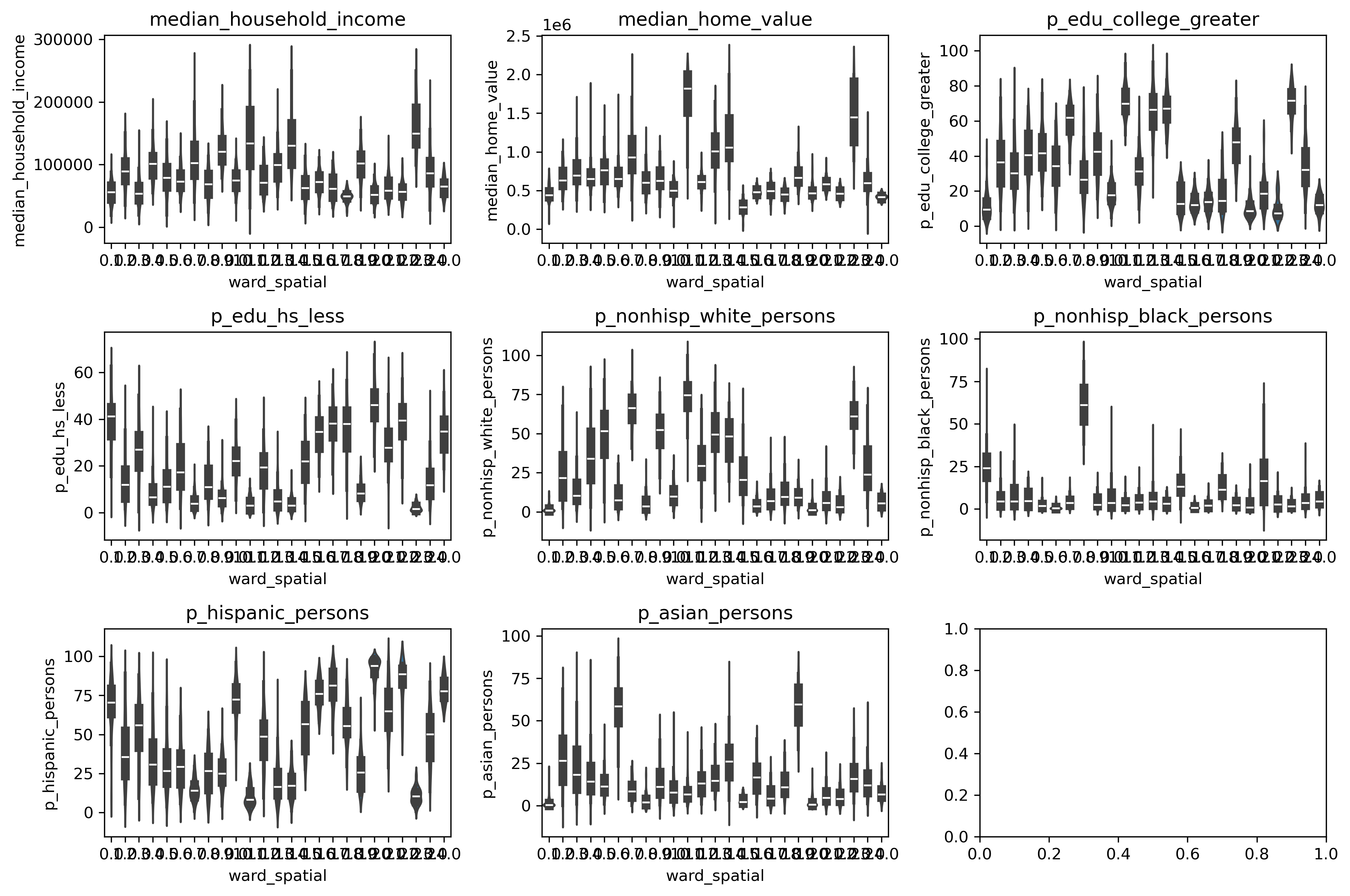
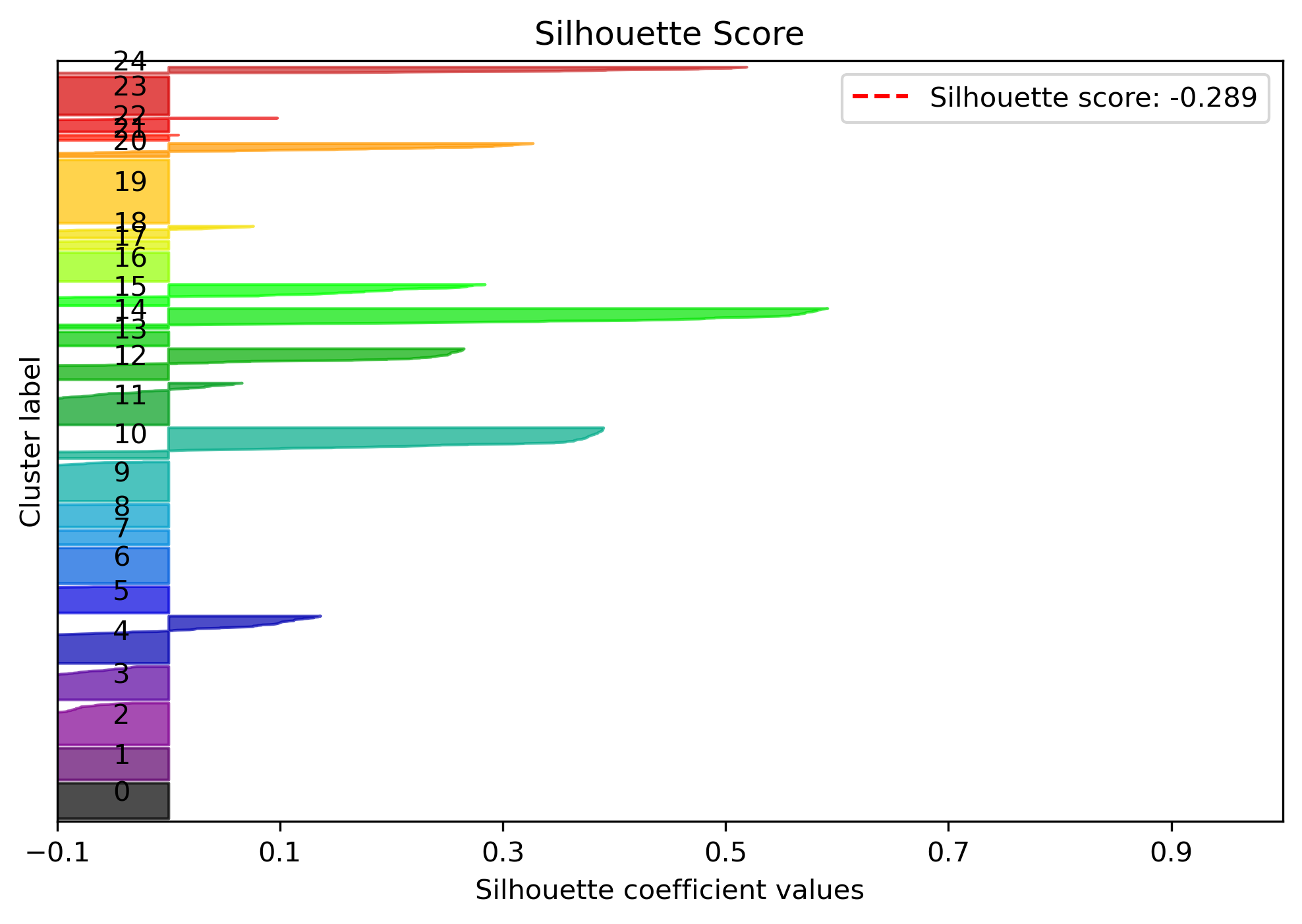
Map of Silhouette Scores for L.A. Regions

Rather than searching for unique types, regardless of where they are in the study area (which is what general clustering algorithms focus on), regionalization algorithms arguably search for unique places in the study area, where uniqueness is defined by the concentration of attribute similarity in space. That is, we are looking for places that are geographically distinct from their neighbors, where members of a single region are relatively similar to one another, but distinctly different from those nearby.

To operationalize these concepts, we leverage the notion of a geosilhouette, which blends the roles of geographic and attribute similarity into a single metric. There are two types of geosilhouettes, depending on whether we are most interested in differences between region cores (path silhouettes) or region boundaries (boundary silhouettes)

Code

la_ward_model[2021].boundary_silhouette.boundary_silhouette.mean()

np.float64(0.09576599634910776)

Code

la_ward_model[2021].path_silhouette.path_silhouette.mean()

np.float64(0.04836626548915017)

Code

la_ward_model[2021].plot_boundary_silhouette(figsize=(5, 5))
la_ward_model[2021].plot_path_silhouette(figsize=(5, 5))

/Users/knaaptime/miniforge3/envs/urban_analysis/lib/python3.12/site-packages/geosnap/visualize/mapping.py:171: UserWarning: `proplot` is not installed.  Falling back to matplotlib
  warn("`proplot` is not installed.  Falling back to matplotlib")
/Users/knaaptime/miniforge3/envs/urban_analysis/lib/python3.12/site-packages/mapclassify/classifiers.py:1767: UserWarning: Not enough unique values in array to form 6 classes. Setting k to 4.
  self.bins = quantile(y, k=k)
/Users/knaaptime/miniforge3/envs/urban_analysis/lib/python3.12/site-packages/geosnap/visualize/mapping.py:171: UserWarning: `proplot` is not installed.  Falling back to matplotlib
  warn("`proplot` is not installed.  Falling back to matplotlib")

There are also many regionalization algorithms to choose from (see the PySAL spopt package for more information on each of them)

Code

cluster_types = [
    "kmeans_spatial",
    "ward_spatial",
    "skater",
    "spenc",
    "azp",
]

from sklearn.preprocessing import MinMaxScaler

f, ax = plt.subplots(2, 3, figsize=(11, 10))
ax = ax.flatten()

for i, k in enumerate(cluster_types):
    df = gaz.regionalize(
        gdf=la,
        method=k,
        columns=columns,
        n_clusters=25,
        scaler=MinMaxScaler(),
        weights_kwargs=dict(use_index=True, silence_warnings=True),
        region_kwargs=dict(gamma=1),
    )
    df.to_crs(3857).sort_values(k).plot(
        k, categorical=True, figsize=(7, 7), alpha=0.6, ax=ax[i]
    )
    ax[i].axis("off")
    ax[i].set_title(k, fontsize=14)
    ctx.add_basemap(ax=ax[i], source=ctx.providers.CartoDB.Positron)
    plt.tight_layout()
plt.show()

Geodemographic Regions in L.A. using Alternative Regionalization Methods

Again, the colors are arbitrary and the patterns (i.e. which tracts get grouped together in a single color) are the important parts

Code

ks_best, ks_table = gaz.find_region_k(
    gdf=la,
    method="ward_spatial",
    columns=columns,
    min_k=2,
    max_k=50,
    return_table=True,
    weights_kwargs=dict(use_index=True, silence_warnings=True),
)

Code

ks_best.T

time_period	2021.0
silhouette_score	2.0
calinski_harabasz_score	2.0
path_silhouette	2.0
boundary_silhouette	50.0
davies_bouldin_score	2.0

Code

ks_table.T.head()

k	2.0	3.0	4.0	5.0	6.0	7.0	8.0	9.0	10.0	11.0	...	41.0	42.0	43.0	44.0	45.0	46.0	47.0	48.0	49.0	50.0
silhouette_score	0.398151	-0.099869	-0.100067	-0.164610	-0.155095	-0.208675	-0.213824	-0.232700	-0.232987	-0.213964	...	-0.353114	-0.350939	-0.362779	-0.377136	-0.376220	-0.414931	-0.414015	-0.425031	-0.440513	-0.438646
calinski_harabasz_score	984.873146	540.893605	561.134923	420.742953	475.288513	396.009640	364.579200	322.961558	287.470732	331.574073	...	164.664134	162.513423	159.203538	161.149831	157.745153	154.314938	152.024407	154.389852	155.331230	154.086244
davies_bouldin_score	1.142351	1.262321	2.388560	15.480583	12.884447	15.430332	5.441137	5.853003	6.417645	7.655067	...	9.978973	11.640883	12.737700	12.429899	16.061967	16.739235	16.571391	17.464038	17.239211	17.601186
path_silhouette	0.285660	-0.096397	-0.067966	-0.004911	-0.014573	-0.011200	0.011880	-0.066787	-0.086747	-0.031066	...	0.044299	0.051075	0.052471	0.053939	0.047712	0.043448	0.045772	0.045859	0.045496	0.058159
boundary_silhouette	0.156863	0.134452	0.156785	0.147162	0.170921	0.160621	0.164475	0.161105	0.154685	0.153457	...	0.196727	0.199428	0.199332	0.203337	0.201914	0.203588	0.203538	0.204954	0.206206	0.206675

5 rows × 49 columns

Code

ks_table.columns

Index(['silhouette_score', 'calinski_harabasz_score', 'davies_bouldin_score',
       'path_silhouette', 'boundary_silhouette', 'time_period'],
      dtype='object')

Code

f, ax = plt.subplots(2, 3, figsize=(15, 10))
ax = ax.flatten()

for i, metric in enumerate(ks_table.columns.values):
    ks_table[metric].plot(ax=ax[i])
    ax[i].set_title(metric)

Whereas the general silhouette score (and the other general cluster metrics) decrease steadily is the number of clusters increases (because we start to split hairs into super specialized types), the geosilhouettes, especially the boundary silhouette generally increase as n_clusters increases because it becomes easier and easier to differentiate units from nearby units as you consider smaller and smaller neighborhoods.

In addition to the set of compositional attributes, a crucial input to regionalization algorithms is the spatial weights parameter (W), which defines the “geographic similarity” between units. Generally, the goal of regionalization algorithms is to define a distinct, contiguous [set of] region(s), which usually means using a contiguity-based W object (and as such, the default W is a Rook weight). But it is also possible to relax the contiguity enforcement using something like a distance-band weight, which would group nearby observations even if they are not necessarily touching each other. Sometimes these results are called “fuzzy regions,” because the boundaries of each region are less strict.

Code

from libpysal.weights import DistanceBand

la_distance_band = gaz.regionalize(
    gdf=la,
    columns=columns,
    method="ward_spatial",
    n_clusters=25,
    spatial_weights=DistanceBand,
    weights_kwargs=dict(threshold=2000),
)

la_distance_band[["ward_spatial", "geometry"]].explore(
    "ward_spatial", categorical=True, tiles="CartoDB Positron"
)

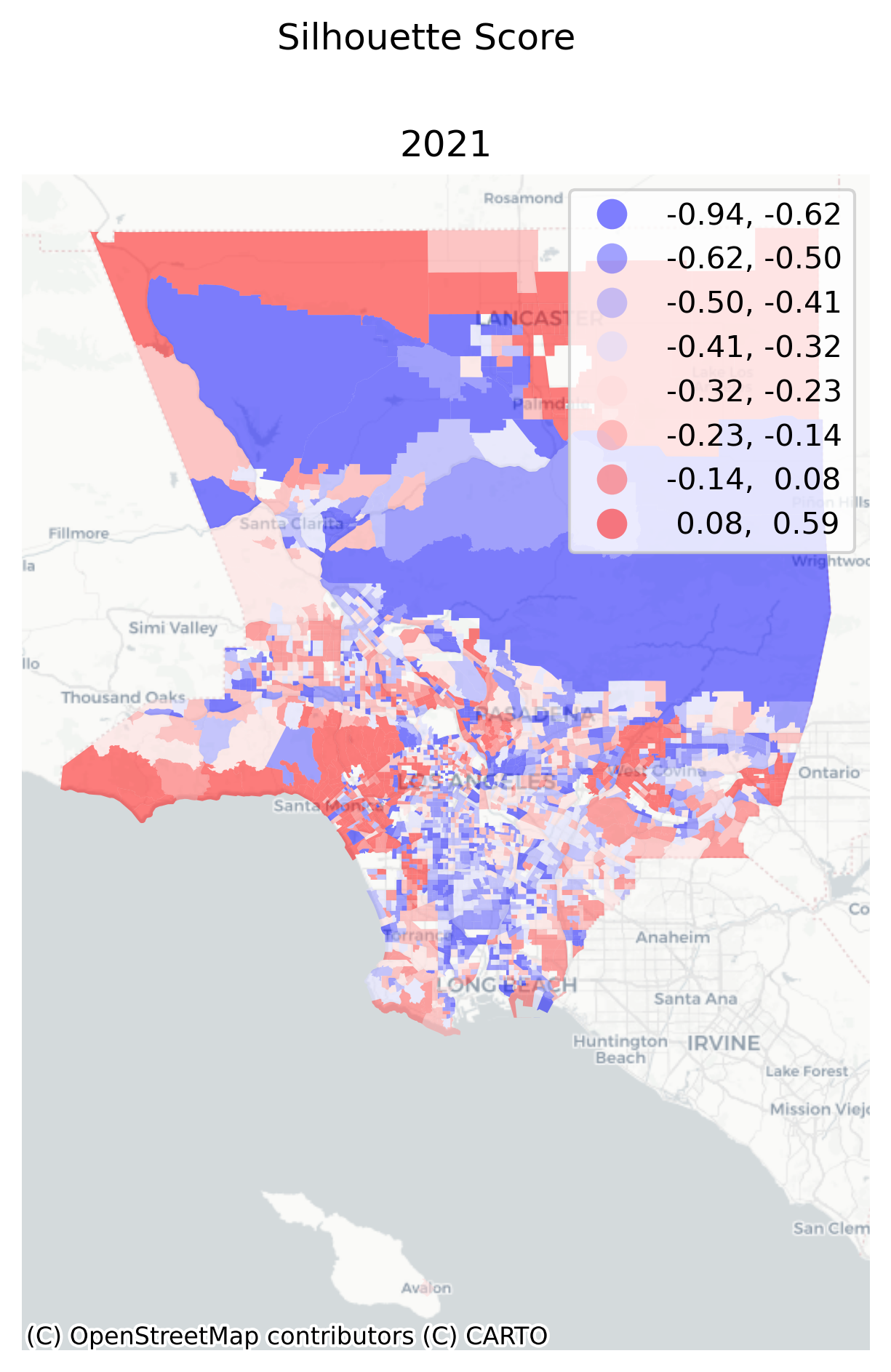
/Users/knaaptime/miniforge3/envs/urban_analysis/lib/python3.12/site-packages/libpysal/weights/util.py:826: UserWarning: The weights matrix is not fully connected: 
 There are 107 disconnected components.
 There are 91 islands with ids: 10, 14, 15, 52, 828, 831, 833, 1012, 1078, 1085, 1086, 1087, 1089, 1146, 1255, 1277, 1283, 1467, 1468, 1471, 1489, 1706, 1944, 2112, 2115, 2117, 2166, 2167, 2168, 2169, 2171, 2174, 2175, 2178, 2179, 2180, 2182, 2183, 2184, 2185, 2186, 2187, 2188, 2189, 2190, 2191, 2193, 2214, 2215, 2221, 2226, 2227, 2228, 2230, 2231, 2232, 2233, 2234, 2236, 2237, 2238, 2242, 2243, 2246, 2260, 2270, 2272, 2273, 2274, 2275, 2276, 2277, 2278, 2284, 2296, 2302, 2303, 2304, 2305, 2306, 2314, 2316, 2317, 2318, 2319, 2321, 2323, 2330, 2331, 2336, 2337.
  w = W(neighbors, weights, ids, **kwargs)
/Users/knaaptime/miniforge3/envs/urban_analysis/lib/python3.12/site-packages/libpysal/weights/distance.py:844: UserWarning: The weights matrix is not fully connected: 
 There are 107 disconnected components.
 There are 91 islands with ids: 10, 14, 15, 52, 828, 831, 833, 1012, 1078, 1085, 1086, 1087, 1089, 1146, 1255, 1277, 1283, 1467, 1468, 1471, 1489, 1706, 1944, 2112, 2115, 2117, 2166, 2167, 2168, 2169, 2171, 2174, 2175, 2178, 2179, 2180, 2182, 2183, 2184, 2185, 2186, 2187, 2188, 2189, 2190, 2191, 2193, 2214, 2215, 2221, 2226, 2227, 2228, 2230, 2231, 2232, 2233, 2234, 2236, 2237, 2238, 2242, 2243, 2246, 2260, 2270, 2272, 2273, 2274, 2275, 2276, 2277, 2278, 2284, 2296, 2302, 2303, 2304, 2305, 2306, 2314, 2316, 2317, 2318, 2319, 2321, 2323, 2330, 2331, 2336, 2337.
  W.__init__(

Make this Notebook Trusted to load map: File -> Trust Notebook

Code

f, ax = plt.subplots(2, 3, figsize=(11, 10))
ax = ax.flatten()
la = la.to_crs(la.estimate_utm_crs())
for i, k in enumerate(cluster_types):
    df = gaz.regionalize(
        gdf=la,
        method=k,
        columns=columns,
        spatial_weights=DistanceBand,
        n_clusters=25,
        scaler=MinMaxScaler(),
        weights_kwargs=dict(use_index=True, threshold=2000, silence_warnings=True),
        region_kwargs=dict(gamma=0.25),
    )
    df.to_crs(3857).sort_values(k).plot(
        k, categorical=True, alpha=0.6, figsize=(7, 7), ax=ax[i]
    )
    ax[i].axis("off")
    ax[i].set_title(k, fontsize=14)
    ctx.add_basemap(ax=ax[i], source=ctx.providers.CartoDB.Positron)
    plt.tight_layout()

Fuzzy Geodemographic Regions using Different Regionalization Algorithms