Code
import os
import contextily as ctx
import geopandas as gpd
import matplotlib.pyplot as plt
import pandarm as pdna
import pandas as pd
import quilt3 as q3
import requests
from esda import Moran, Moran_Local
from geosnap import DataStore
from geosnap import analyze as gaz
from geosnap import visualize as gvz
from geosnap import io as gio
from IPython.display import Image
from libpysal.graph import Graph
from mapclassify import classify
from scipy.stats import zscore, chisquare
from semopy import Model, calc_stats, semplot
from segregation.local import LocalDistortion, MultiLocalEntropy
from tobler.area_weighted import area_interpolate
from zipfile import ZipFileOMP: Info #276: omp_set_nested routine deprecated, please use omp_set_max_active_levels instead.

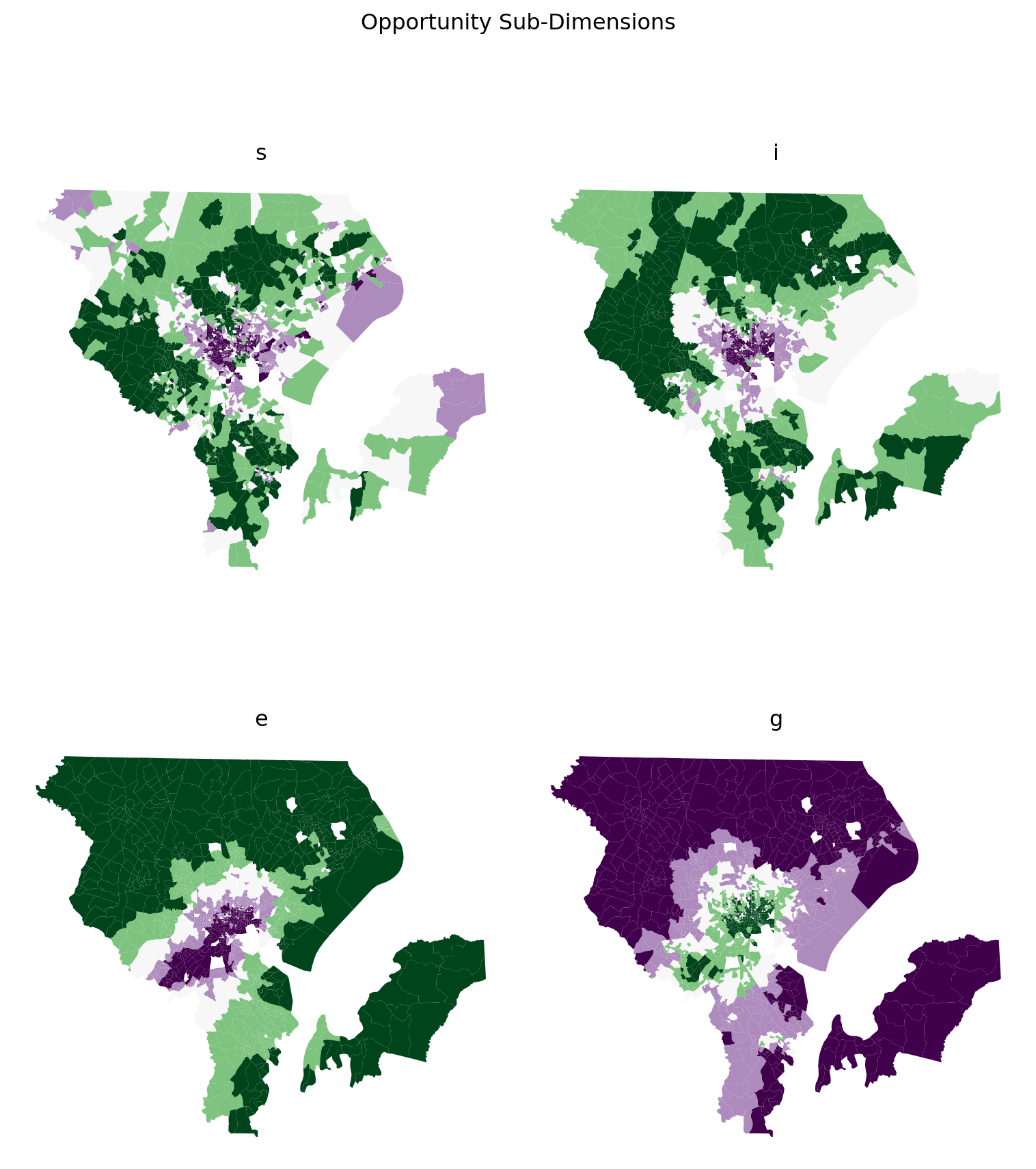
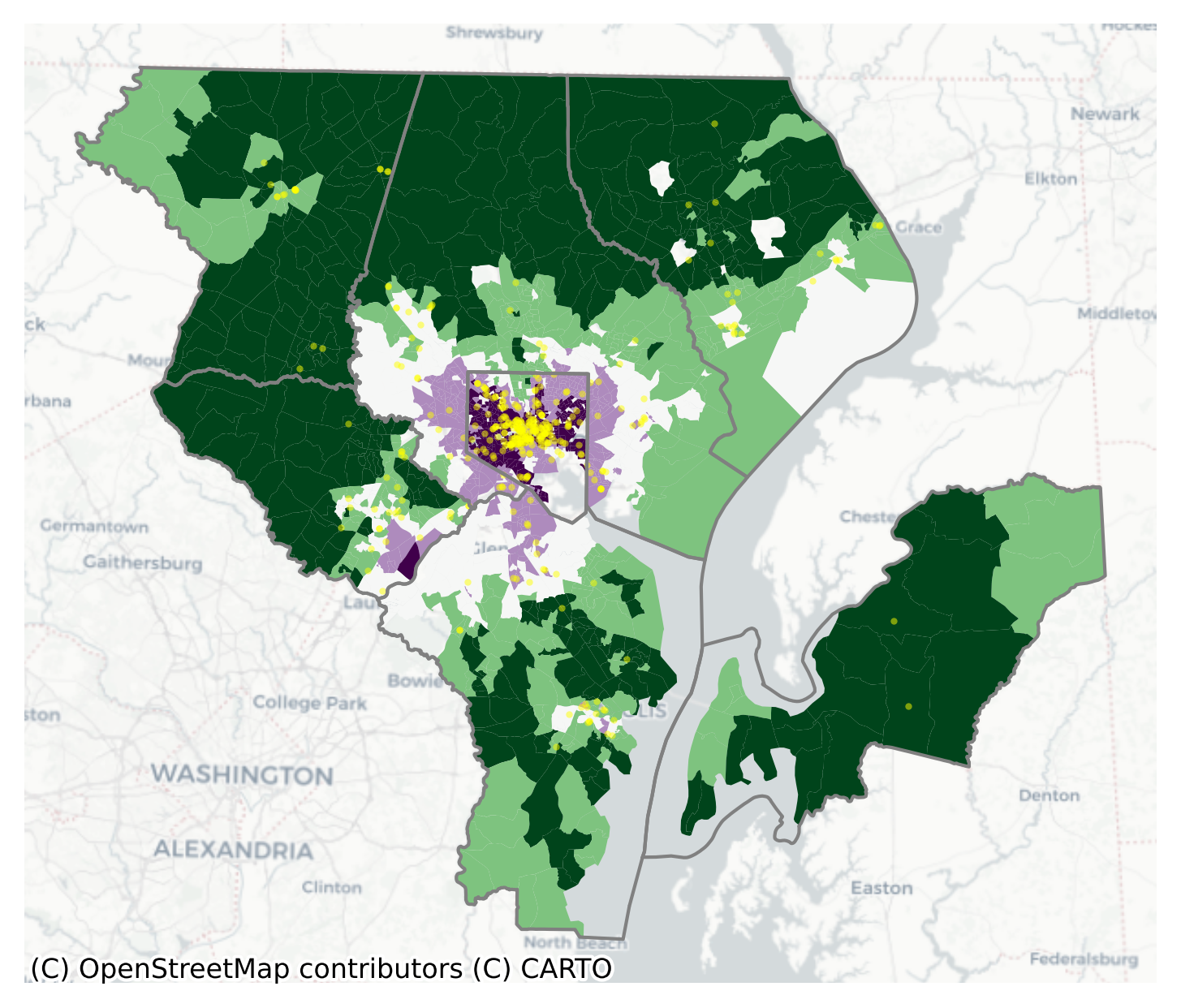
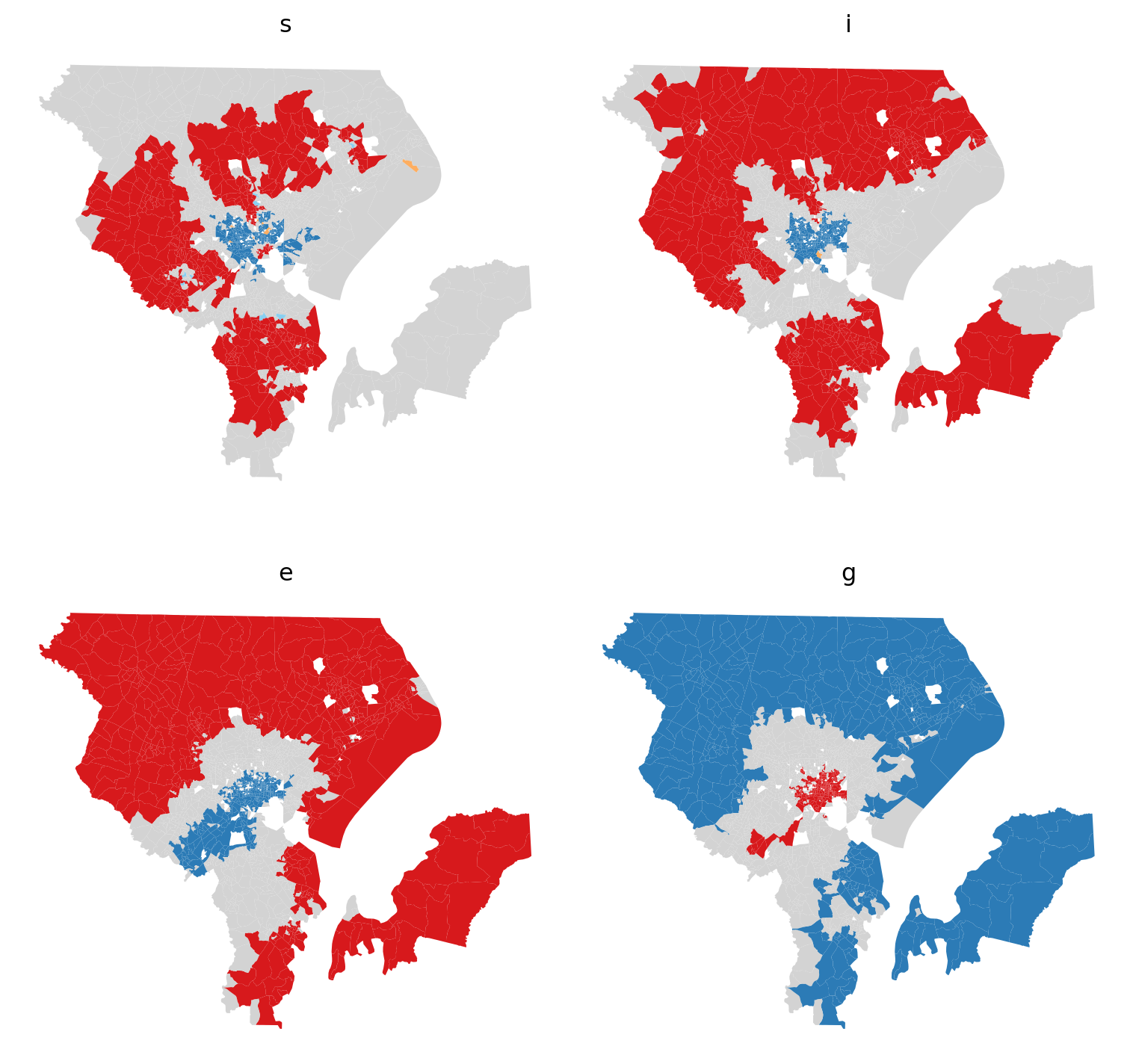
21.1.1 social data
As usual, our only option for social data at this scale comes from the Census, and we will use blockgroup geometries to narrow down the spatial scale as much as possible. This will cost us a few variables that are available at the tract level, so you could also re-do this analysis by moving up a level. The variables in this category are designed to capture the ways that social interactions help you get ahead. Historically, the focus has been on the negative consequences of being in the bottom of the distribution (the negative effects of concentrated poverty), though some have also called for increasing attention on the other end, and the importance of concentrated affluence which helps those in privilege remain there (Sampson et al., 2015).
Here, we will say that socioeconomic status increases local opportunity, with SES measured by income and educational attainment for adults. We will also say that racial integration promotes opportunity, so we include the local distortion segregation measure.
Code
Code
Since the CFA model is designed to model the covariation among the set of input variables, we can also check to see how correlated our chosen set looks.
Code
And this looks as we would expect; income and education are positively correlated, whereas segregation has a weaker negative correlation with the other two.