flowchart TD
subgraph j
Xj --> yj
ej((ej)) -.-> yj
end
subgraph i
ei((ei)) -.-> yi
Xi --> yi
end
30 Graphical Spatial Models
In the DAG and causal inference literature errors are typically left out (Pearl, 2014). In Bayesian statistics and especially in Structural Equation Modeling, errors are considered explicitly and formulated as part of the problem. In my view, causal inference people, Bayesians, and SEM folks all use path diagrams and graphic models similarly, but with their own distinct flavors (Clark, 2018). Spatial models are not well-suited to DAGs because we are often interested in cyclical models with feedback, and it is also useful to represent errors explicitly. In general, spatial econometric models are a kind of equilibrium model with simultaneity, where Huntington-Klein (2022) argues DAGs and do-calculus are probably less useful than traditional econometric techniques.
Standard causal diagrams must be acyclic, whereas equilibrium models contain feedback loops and so are cyclic. The difficulty that standard causal diagrams have with equilibrium models was a particular concern in the Imbens (2020) review of SCM.
– Huntington-Klein (2022), p.332
Without a doubt, Pearl (2023) would disagree :P. However the spatial models we need to consider and contrast are either semi-Markovian (in the spatial error, et al case) or non-Markovian (in the spatial lag et al case) (Pearl, 1998) because they contain cycles and feedback loops.
One fundamental property of Markovian models is parent screening: given the state of its parents \(pa\), each variable \(X\); is conditionally independent of all its nondescendants in the graph. This follows immediately from the independence of the errors \(\epsilon\); and supports the intuition that once the direct causes of \(X\); are known, the probability of \(X\); is completely determined; no other event preceding \(X\); could modify this probability. As a result, the statistical parameters of Markovian models can be estimated by ordinary regression analysis.
– Pearl (1998), p.237
In many spatial models this is not the case, so we need extra techniques like instrumental variables regression to estimate the model and the pure graphic representation gets complicated at best (Huntington-Klein, 2022). Thus, the graphic spatial models shown here are closer to the Structural Equation Model flavor than the SCM flavor (though I don’t bother including errors for every measure) (Bollen, 2014; Coman et al., 2015; SPIRTES et al., 1998).
The SEM (and Bayesian) perspective also helps reconcile this style with the causal style because the former group tends to think of a dependent variable \(y_i\) as a measurement rather than an actual outcome. Thus the resulting measure \(y_i\) is caused by a DGP that includes error by definition–nothing is measured perfectly–in which case the model needs to show how error causes the outcome1. Representing error explicitly and at the start is useful for considering whether it is entirely random in its contribution to \(y_i\), or whether some parts are structured (and therefore also need to be modeled explicitly). I think this is also codifying error using the ‘conceptual interpretation’ from Pearl (1998), which is useful precisely in our current case (even if errors are designed to work in the SCM framework via the ‘operational definition’)2 e.g.
“when it comes to deciding whether pairs of error terms can be assumed to be uncorrelated. Because such decisions are needed at a stage when the model’s parameters are still “free,” they cannot be made on the basis of numerical assessments of correlations but must rest instead on qualitative structural knowledge about how mechanisms are tied together and how variables affect each other.”
– Pearl (1998), p.274
Spatial models also depend critically on interactions which can be difficult in traditional DAG language so I include spatially-interactive variables (like spillover and propagation) as distinct nodes following Clark (2018) and Attia et al. (2022), though technically, this is breaking the rules (Huntington-Klein, 2022). As an additional difficulty, the spatial relationship graph \(W\) is itself a specific kind of interaction variable that is technically unobserved (albeit strongly inferred), then subsequently interacted with other variables to produce \(WX\), \(Wy\), and \(WU\). The fact that \(W\) is essentially posited means its worth considering as a path because it affects how elements propagate through the system (and we might/should posit alternatives).
Adpoting the definition of structural parameters from Pearl (1998), these are very different models:
OLS \[y_i = f(X_i, \epsilon)\]
Spatial Lag of \(X\) \[y_i = f(X_i, WX_j, \epsilon)\]
Spatial Error \[y_i = f(X_i, Wu_j, \epsilon)\]
Spatial Lag \[y_i = f(Wy_j, X_i, \epsilon)\]
SLX-Error \[y_i = f(X_i, WX_j, Wu_j, \epsilon)\]
Spatial Durbin \[y_i = f(Wy_j, X_i, WX_j, \epsilon)\]
Notably, LeSage & Pace (2009) LeSage & Pace (2014), and LeSage (2014a) reiterate this point continually.
30.1 Spatial Models as Graphs
Assuming spatial units \(i\) and \(j\), I think about the processes for these respective units as:
- independent if no node from process \(j\) affects \(y_i\)
- interdependent if an ancestor of \(y_j\) also affects \(y_i\)
- co-dependent if \(y_i\) and \(y_j\) share a node simultaneously
This assumes spatial homogeneity which means the \(i\) and \(j\) relationships are symmetric (i.e. the errors for \(i\) and \(j\) are identically distributed), in which case the micro-level processes for each unit \(i\) and \(j\) might look as follows:
30.1.1 Aspatial (OLS)
The outcome \(y_i\) is determined by exogenous variables \(Xi\), and random error \(e_i\). \(y_i\) is independent of anything happening to \(j\) (and vice-versa). The edges are relationships that we estimate, so
\[X_i \rightarrow y_i = \beta,\]
but we actually estimate the error associated with \(y_i\), not the relationship between \(e_i\) and \(y_i\), so
\[e_i \rightarrow y_i = 1 \]
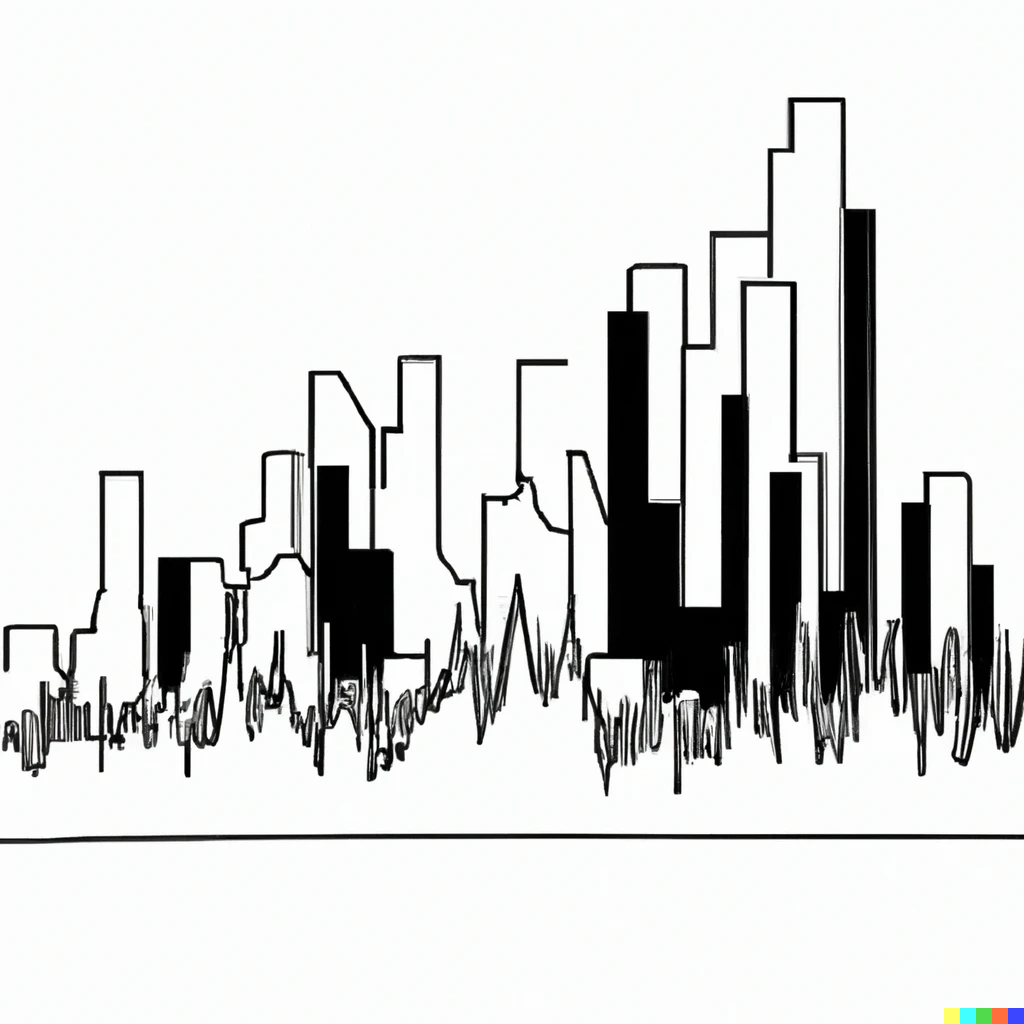
In an aspatial model, the process is the same for every unit. There is an identical model for \(i\) and (every other) \(j\) where edges never cross between \(i\) and \(j\) (so \(X_i \rightarrow Y_i = X_j \rightarrow Y_j = \beta\)); they function as independent co-processes. Our concern is only what influences \(y_i\), so there is no need to care about any \(j\). Generally, this would be represented as a single graph rather than two graphs with subscripts (because why duplicate if the models are identical for each unit?). But it is useful to represent the independent co-processes here because with spatial models we need to consider \(j\).
Given Tobler’s law (and many other theoretical considerations), there is often good reason to believe that \(i\) and \(j\) are not independent. So the baseline test is to see whether \(e_i \leftarrow W_{ij} \rightarrow e_j\) exists, e.g. using a Lagrange Multiplier test (Anselin, 1988; Anselin et al., 1996), because proving that link provides evidence of spatial interaction (and invalidates an aspatial model). The tests can be performed separately for different links (lag vs error), or multiple links (lag and error), and have both classic and robust forms.
flowchart TD
subgraph j
Xj --> yj
ej((ej)) -.-> yj
end
subgraph i
ei((ei)) -.-> yi
Xi --> yi
end
ej<-->Wij{Wij}
ei<-->Wij{Wij}
If this link exists, then a different model is necessary to estimate relationships accurately. The trouble is, there are many reasonable conceptual models that could induce that link, and applied researchers are faced with the task of choosing ‘the best’ among several plausible alternatives. There are different strategies for this; some suggest starting with simple models, testing for the existence of the link, and incrementally building up to more complex models (specific to general), while others prefer to start with fully-specified models, then systematically remove complexity when the relationships are deemed unnecessary (general to specific). (Anselin et al., 2024; LeSage, 2014b; LeSage & Pace, 2014). In a recent simulation exercise, Anselin et al. (2024) suggest that there is no single ‘best’ strategy, but in general, forward-based searches (specific to general) are preferred.
30.1.2 SLX Model
flowchart TD
W{"`$W_{ij}$`"} --> WXi
W{"`$W_{ij}$`"} --> WXj
Xj --> WXj
Xi --> WXi
subgraph j
WXi --> yj
ej(("`$\e_j$`")) -.-> yj
Xj --> yj
end
subgraph i
Xi --> yi
ei(("`$\e_i$`")) -.-> yi
WXj --> yi
end
The SLX model includes exogenous of \(Xj\) through the spatial graph \(W_{ij}\). The process for \(i\) is no longer fully independent of the process for \(j\) as in the aspatial model above, but \(y_i\) depends on the exogenous characteristics of \(j\), \(WXj\). I might hazard to call these interdependent processes. Even though \(i\) and \(j\) interact, they do so only through the exogenous variables; they have no nodes in common (apart from \(W_{ij}\), which connects them by definition, but only in concept), so you can still draw a box around each process–you could pull \(WXj\) into the \(i\) box and treat it as part of the \(i\) process. Here \(WX_j \rightarrow y_i =\theta\) is local spatial spillover. Again, since the focus is really on the inputs to \(y_i\), displaying \(e_j\), \(WXi\), and \(y_j\) is not necessary but the full diagram is useful for thinking about the system and comparing the model to others.
30.1.3 Spatial Error Model
flowchart TD
subgraph j
Xj --> yj
ej
end
WU((WU))
W{"`$W_{ij}$`"} --> WU
subgraph i
Xi --> yi
ei
end
ei((ei)) <-.-> WU
ej((ej)) <-.-> WU
W
WU -.-> yj
WU
WU -.-> yi
In the spatial error model (SEM, though not to be confused with structural equation model in this particular context), the error at location \(i\) is affected by the error at location \(j\). The infinite loop in path \(e_i \rightarrow WU \rightarrow e_j \rightarrow WU \dots\) is global error propagation. In this case, the process for \(i\) shares an endogenous element with the process for \(j\), which I would call co-dependent because \(i\) and \(j\) interact through a shared variable simultaneously3 and the nodes cannot be separated between the \(i\) and \(j\) processes. This is distinct from a multilevel model where \(i\) and \(j\) belong to different groups (as sometimes shown in the SCM framework) because \(e_i\) and \(e_j\) contain a simultaneous feedback (Wolf et al., 2021).
The path coefficients for the errors are fixed to one and we estimate the error \(U\). If this is the true model, then estimating it via OLS effectively ignores the path \(e_j \rightarrow WU \rightarrow e_i\), which throws off the estimate for \(U\). That is, using OLS misjudges the error going into \(y_i\), which makes the estimate of \(\beta\) inefficient, but not biased. There are no missing paths, but the size of the error is mis-estimated. Assuming spatial homogeneity (and that \(W_{ij}\) is known), then we can separate out
\[e_i \rightarrow WU = \epsilon_i\]
and
\[e_j \rightarrow WU = \lambda\]
and
\[WU \rightarrow y_i = 1\]
As with before, the nodes \(X_j\) and \(y_j\) (and their associated edges) are not technically necessary.
30.1.4 Spatial Lag Model
flowchart TD
Wy((Wy))<-->yi
subgraph j
ej((ej)) -.-> yj
Xj --> yj
yj
end
subgraph i
Xi --> yi
ei((ei)) -.-> yi
yi
end
W{"`$W_{ij}$`"}--> Wy
Wy<-->yj
The spatial lag model includes endogenous interaction between \(y_i\) and \(y_j\) through \(W_{ij}\). This is another model with a node shared simultaneously between \(i\) and \(j\), this time representing what I might call co-dependence. The infinite loop \(y_i \rightarrow Wy \rightarrow y_j \rightarrow Wy \dots\) is global spatial spillover (Anselin, 2002). If this is the true model but it is estimated with OLS, you are effectively ignoring \(y_j \rightarrow Wy \rightarrow y_i\) which is an omitted path into \(y_i\). This induces the usual omitted variable bias, but also exacerbates any other OVB misspecification because of the feedback loop through \(Wy\) (LeSage & Pace, 2009). A critical implication of the SAR model is that every X variable has an indirect effect because of the feedback path \(X_i \rightarrow y_i \rightarrow Wy \rightarrow y_i\), sometimes called the spatial multiplier (Anselin, 2002, 2003; Steimetz, 2010) (hence the amplification of OVB).
- Direct Effect: \(X_i \rightarrow y_i\)
- Indirect Effect: \(X_i \rightarrow y_i \rightarrow Wy \rightarrow y_j \rightarrow Wy \rightarrow y_i\)
In the indirect effect, the \(X_i\) variable is transmitted back to \(y_i\) through \(y_j\). In this case, \(X_j\) and \(e_j\) can be omitted because they are not necessary in the model for \(y_i\) (assuming you can instrument for Wy). In the case of spatial heterogeneity, though, either or both terms would result in a different estimate for \(y_j\) which would propagate to \(y_i\) (!). Assuming \(i\) and \(j\) are symmetric, then \(X_i\) has the same influence on \(y_i\) that \(X_j\) has on \(y_j\), etc. Thus \(X_j\) and \(e_j\) can be removed from this graph.
30.1.5 SLX-Error Model
flowchart TD
W{"`$W_{ij}$`"} --> WXi
W{"`$W_{ij}$`"} --> WXj
Xj --> WXj
WU((WU))
subgraph j
ej
WXi --> yj
Xj --> yj
yj
end
subgraph i
Xi --> yi
WXj --> yi
ei
end
Xi --> WXi
ei((ei)) <-.-> WU
ej((ej)) <-.-> WU
W
WU -.-> yj
WU
WU -.-> yi
W-->WU
The SLX-Error model has the same endogenous error propagation as the SEM, and also the exogenous effects from the SLX model. There is one shared node in the processes, but only error. The \(WX_i\) and \(y_j\) nodes can be removed from this graph.
30.1.6 Spatial Durbin Model
flowchart TD
Xj-->WXj
Wy((Wy))<-->yi
subgraph j
Xj --> yj
WXi-->yj
ej((ej)) -.-> yj
yj
end
W{"`$W_{ij}$`"}--> Wy
subgraph i
Xi --> yi
WXj-->yi
ei((ei)) -.-> yi
yi
end
Wy<-->yj
Xi-->WXi
The SDM model has the exogenous spillover from the SLX model and the endogenous spillover from the SAR model. As with the lag model the \(i\) and \(j\) processes share the \(Wy\) node. The \(WX_i\) and \(e_j\) nodes can be removed from this graph.
30.2 Spatial (Process) Heterogeneity
The adage with regression is that resulting errors must be i.i.d, independent and identically distributed to meet the model’s assumptions (i.e. to produce the intended result). In the graphs above, we explore different ways to ensure the independence criterion by breaking the link between \(e_i\) and \(e_j\). The second clause, however, requires errors to be identically distributed, which means the spatial processes (and \(\beta\) relationships) are the same for units \(i\) and \(j\). But as with treatment heterogeneity (Gelman et al., 2023), sometimes \(i\) and \(j\) processes are actually different (because they are different places after all).
In this case, the boxes for \(i\) and \(j\) are different because they represent different processes. Geographically-Weighted Regression takes this idea to the extreme: it assumes there is no co-dependence between \(i\) and \(j\), but instead there is an entirely different model for each \(i\) (estimated via a subsample of the data defined by \(W_{ij}\)). That means in GWR each unit has a different DGP, and there is no concept of spatial interaction. Every \(i\) box in the diagrams above is unique in such a case. Both of those properties are major drawbacks, in my opinion, because we are often interested in the average process (not unique processes for each unit) and in spatial interaction, but GWR does not explain either one.
The spatial econometric view of spatial heterogeneity is to test for error heteroskedasticity. If the errors are heterogeneous, then there are two options:
- use a more robust significance test on the estimated coefficients
- fit a model using spatial regimes
The former option does not require fitting a different model; in this approach, the errors are still viewed as fundamentally random, just improperly estimated, so the significance of the coefficients is evaluated more consevatively (Anselin, 1990; Arraiz et al., 2009; Kelejian & Prucha, 2010).
The latter option views the error heterogeneity as potentially systematic, and resulting from different spatial processes. Thus, the second approach breaks the study region into smaller sections and fits unique regression models in each region. This is a middle ground between a global model like SAR and a hyperlocal model like GWR. Regimes are typically specified exogenously, for example in a study using U.S. counties, we might expect slightly different spatial processes to occur in each state or different regions of the country, so regimes would be specified by state/region (Duque & Hierro, 2016; Elhorst & Fréret, 2009; Flores & Rodriguez-Oreggia, 2014; Myers et al., 2015). Alternatively, regimes can be viewed as endogenous, which is an emerging frontier in spatial econometric research (Anselin & Amaral, 2023)
I think this is, like, the heart of Bayesianism, but I am not actually smart enough to make that assessment…↩︎
I am trained as a quantitative social scientist, but am neither a mathemetician, statistician, nor causality expert, so take this with a grain of salt. But in my judgment, the purpose of DAGs and do-calculus a-la the Pearl style is to express a stochastic process as a deterministic process. This is intentional because it divorces the statistical estimation from the philosophical DGP; the whole purpose is to determine whether you can identify \(X\) (a binary decision), regardless of how well you can quantify the precision of that estimate (a continuous decision). In econometric terms, this implies DAGs are concerned exclusively with consistency, and in this context, efficiency is a statistical concern, and therefore irrelevant at this point of the formulating the methods (so the argument goes, anyway). After you have your path diagram set, then you worry about the distribution of \(\epsilon\) (and how to estimate the graph’s edges).↩︎
Hence the proper name for this model, the simultaneous autoregressive error model↩︎